Linear Conversion of Conductivity To Salinity
Looking For a Reliable Conductivity Sensor?
Check out the pHionics STs Series Conductivity. It has a 4-cell electrode for improved stability along with an isolated, 4-20 mA transmitter for high accuracy, durability, and almost no maintenance over 10+ years of service. pHionics also provides a 2-year warranty covering the entire instrument.
Disclaimer: This article covers an equation for linear scaling of conductivity sensors to estimate salinity based on the Practical Salinity Scale of 1978 (PSS-78). The equation effectively estimates seawater salinity between the practical salinity ranges of 22 and 42, temperatures 5-35°C, and pressure less than 200 dBar, using a temperature-compensated conductivity sensor. This is not for use in any scientific literature but allows dataloggers and receivers with linear scaling to estimate salinity in real-time.
Purpose
This article provides a simplified means of converting the conductivity of surface seawater (not fresh or brackish water) to salinity for general monitoring purposes. The current standards, PSS-78 and Thermodynamic Equation of Seawater – 2010 (TEOS-10), are available online, but use complicated equations and programs such as MATLAB that are not accessible to everyone. Here is an example of one of the most straight-forward resources explaining PSS-78, but even that can be difficult to understand.
Conductivity to salinity calculators based on PSS-78 are available online, but very few of them have batch processing capabilities and none can be used when monitoring conductivity in real-time with instruments that require linear scaling (e.g. The HOBO RX3000 with a 4-20 mA sensor). Here, we lay out our logic and method of creating a linear equation that allows temperature-compensated conductivity sensors to estimate salinity of surface seawater (practical salinity values of 22-42 at 0-200m depth and 5-35°C) within 5% of the true value. The equation is provided below and the rest of the article explains how it was derived and why there are limitations to its use.
The Linear Equation for Converting Conductivity to Practical Salinity
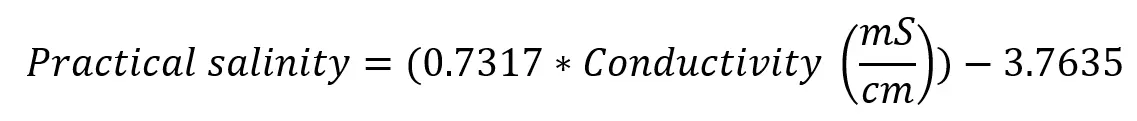
Brief History
Salinity is defined as a measure of dissolved salts in a concentration of water while conductivity is defined as the ability of an aqueous solution to transfer an electrical current. Aqueous solutions transfer electrical currents better with higher concentrations of ions, which are directly related to the amount of dissolved salts in the water. The relationship is not perfect as each ion has a different level of conductivity and, therefore, a different ratio between conductivity and dissolved salts depending on the concentration of each ion. For this reason, salinity can be most accurately calculated from aqueous solutions with known conductivity ratios. While fresh and brackish water vary significantly in terms of ion concentrations, seawater has a fairly stable composition, allowing for creation of a standard equation relating conductivity to salinity. This is called the Practical Salinity Scale of 1978 (PSS-78).
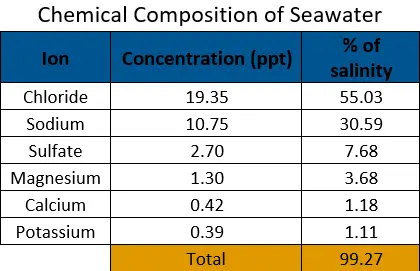
PSS-78 was derived from the research of Edward Lewis, replacing the less accurate chlorinity scale. It can be viewed here but is not easily comprehensible and is not linear. PSS-78 uses conductivity (µS/cm), temperature (°C), and pressure (dBar) measurements to calculate salinity from 2-42 (practical salinity has no units but is very close to ppt) within the temperature range of -2°C to 35°C and pressure 0-10,000 dBar. It has since been modified by TEOS-10 for practical, but not archival, use.
TEOS-10 outlines Absolute Salinity (SA), which corrects practical salinity values by roughly 0.5% based on location. It effectively accounts for the compositional changes of seawater based on latitude and longitude, along with temperature and density.
While the small corrections to salinity may not seem significant to some applications, it does have larger implications for thermodynamic-related properties such as density, sound speed, and heat capacity of seawater. TEOS-10 is accessible through MATLAB, with instructions for installation and use found here.
As practical salinity is reliant on fewer variables, it is easier to linearize than TEOS-10, which is why we focus on practical salinity instead of absolute salinity for the remainder of this article.
Linearizing Practical Salinity
Practical salinity is dependent on three factors: conductivity, temperature, and depth. Let’s look at the effect of depth on salinity using one of the calculators available online (while the calculations were not done by pHionics, they were referenced to three other PSS-78 salinity calculators online to verify consistency).
List of Calculators:
PSS-78
https://incois.gov.in/Tutor/Utilities/salcon.html
https://jsta.shinyapps.io/cond2sal_shiny/ (good for batch processing but found to have issues when the temperature is not 25°C)
http://www.fivecreeks.org/monitor/sal.shtml
https://reefapp.net/en/salinity-calculator
TEOS-10
https://monrecifamoi.saulme.fr/salinite/sea_water_calculator_teos10.php
Pressure and Practical Salinity
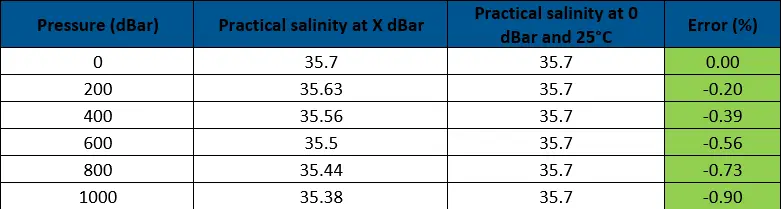
As shown by the tables, the change in practical salinity by pressure is approximately 0.06 per 200 dBar (1 dBar is approximately equal to 1 m depth). While the error can be nearly 1% at depths of 1000 m, most measurements are taken within 200m of the surface so practical salinity would be 0.25% off at most. As we are looking to have an error of less than 5% of the true value, we can ignore change in salinity with pressure up to at least 200 dBar, based on these numbers.
Temperature and Practical Salinity
The next factor is temperature. While temperature has a large effect on salinity, it can be accounted for by using a conductivity sensor with automatic temperature compensation (ATC), which typically standardizes the conductivity output to 25°C. The method of temperature compensation depends on the manufacturer and model but many use a linear temperature coefficient of 2% per °C from 25°C (including pHionics). For seawater, the temperature coefficient ranges from 1.8-2.1%, with lower temperatures and salinities approaching 1.8%. More on calculating the compensation factor can be found in our article on Conductivity Electrodes.
Let’s look at how temperature compensation can affect accuracy over a range of temperatures:
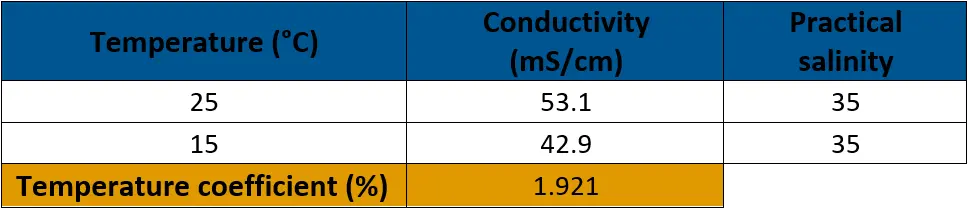
Equation 1. Calculating temperature coefficient to standardize conductivity measurements
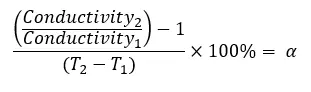
Calculating the Temperature Coefficient in PSS-78
The practical salinity value of 35 at 15°C and 25°C was entered into a calculator that gave conductivity measurements based on the PSS-78 equation. Equation 1 was used to derive the temperature coefficient.
Accuracy of ATC (2%) Conductivity Measurement Compared to PSS-78 Calculated Temperature Coefficient Over 5-35°C

The second table calculates the percent error of conductivity outputs when comparing the temperature coefficient used in PSS-78 (1.9%) to the commonly used temperature coefficient in conductivity sensors (2.0%). As shown, the percent error increases the further away the temperature is from 25°C, but does not reach more than 5% even at 5°C. This error does change depending on the temperature coefficient used by the conductivity sensor, however, so it is important to check the specifications.
As ATC effectively standardizes the conductivity output to 25°C within our acceptable margin of error (5%), temperature change can be eliminated as a variable in practical salinity calculations.
Finding The Linear Relationship
Now that temperature and depth constants (25°C and less than 200 dBar, respectively) have been determined, the only variable left is conductivity, allowing for the equation to be linearized.
To do this temperature of 25°C, pressure of 0 dBar, and conductivity values of 4-62 mS/cm were entered into one of the calculators online that allowed batch processing to obtain practical salinities from 2-42. These values were graphed and a trendline was calculated in Excel, giving a linear equation for the relation between conductivity and salinity, as shown below.
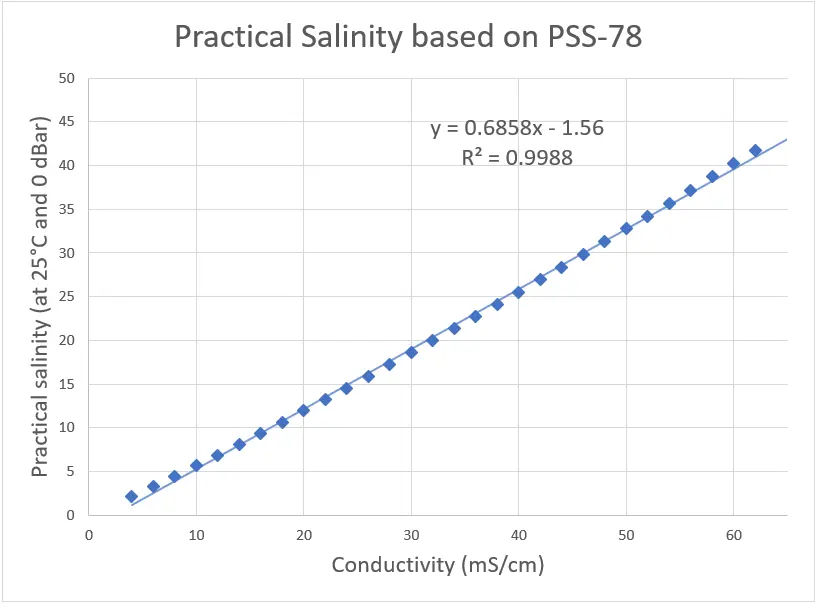
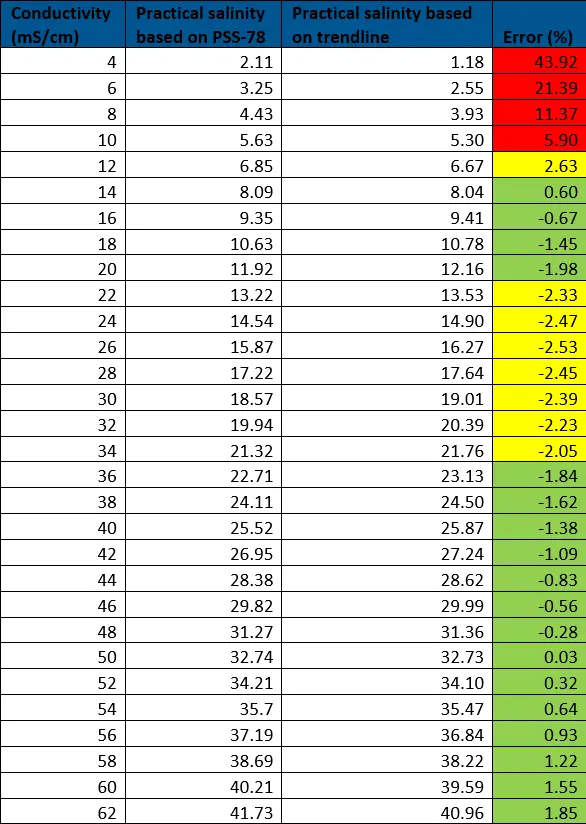
As the trendline has an R2 value of 0.9988, it is a relatively close match. To confirm this, the percent error was calculated, comparing the values based on the PSS-78 calculators to those from the trendline. From this data, we can see that the lower ranges (2.11-5.63) have errors larger than 5% so this linear equation is not usable for low salinity ranges. Any errors of greater than 2% are highlighted in yellow and are seen below 22 practical salinity, defining the low range of our linear equation.
The goal of this article is to provide a reasonably accurate estimate for surface seawater salinity, which has a standard range between 32 and 37 practical salinity. By eliminating the lower salinity values (<22) that affect the trendline, it is possible to achieve a more accurate equation for the standard ranges of seawater. Higher accuracy is confirmed by the higher R2 value (0.9998) compared to the previous value (0.9988). The graph and supporting data are shown below.
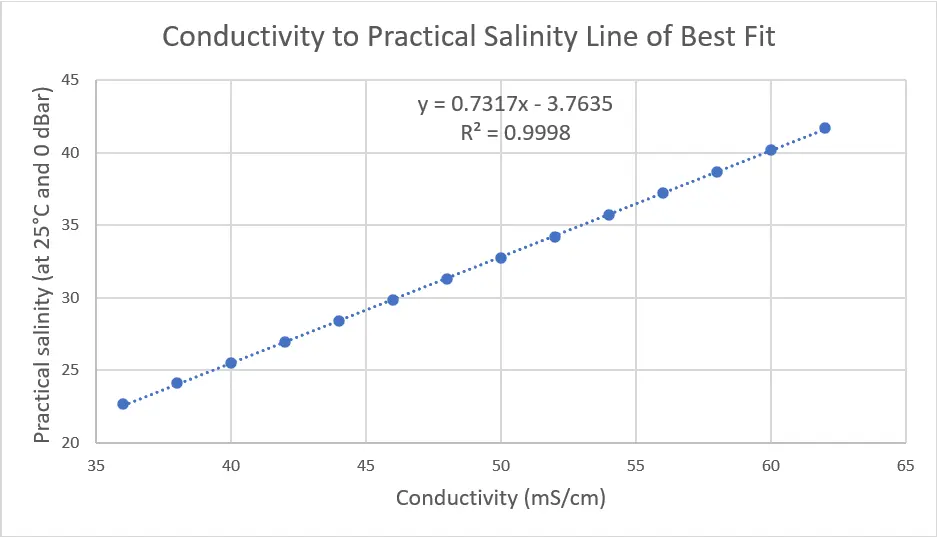
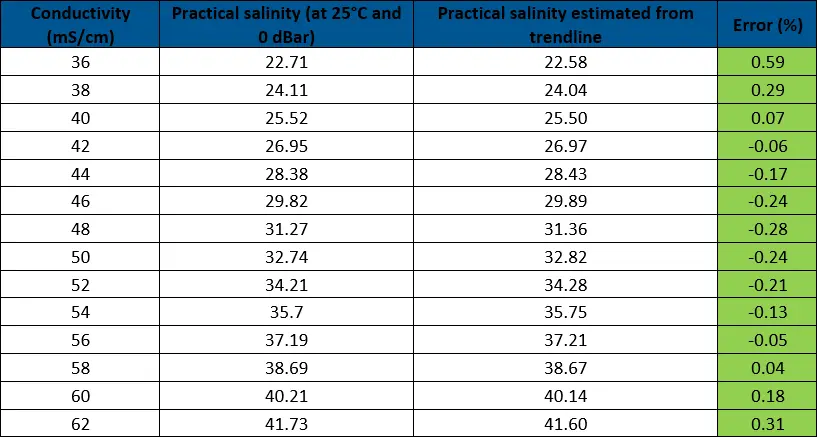
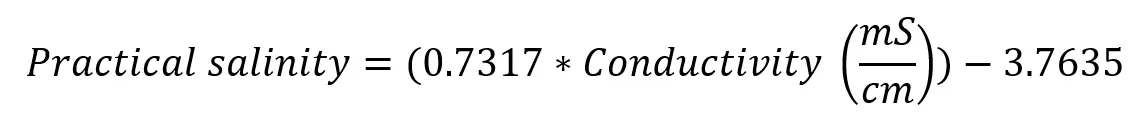
The linear equation for estimating practical salinity has now been tested and confirmed to be within 5% accuracy. The largest room for error comes from the conductivity sensor temperature compensation, so it is important to be aware of the percentage to understand what the possible error is from PSS-78, especially at temperatures close to 0°C.
Conclusion
This equation is designed for dataloggers or any program that provides linear scaling for conductivity measurements with a temperature-compensated sensor. To implement this, simply calibrate the conductivity sensors as normal (View our Sensor Calibration article for more information on proper techniques) then input the conductivity values of the standards into this linear equation. Enter the obtained values into the scaling program and now the conductivity sensor is a practical salinometer.
Again, the obtained practical salinity values should not be substituted instead of PSS-78 or TEOS-10 standards in scientific literature, but properly understanding and programming these standards require a specialized skillset or extensive time to develop the skillset, which is not available to everyone. Current resources online are useful for single data point entry or batch entry, but they can only be done once data is exported, so the derived linear equation presented in this article provides a means of real-time salinity estimation accessible to anyone and usable with most devices.
In summary, the following equation estimates (<5% error) practical salinity for conductivity measurements taken with a temperature-compensated sensor at less than 200 dBar and temperature ranges of 5-35°C (for pHionics instruments and any others with 1.8-2.0%/°C temperature coefficient. 15-35°C range for sensors with <1.8% or >2.0%).
An example of entry into a scaling program can be found below after calibrating with 0 and 50 mS/cm calibration standards.
Conversion to practical salinity

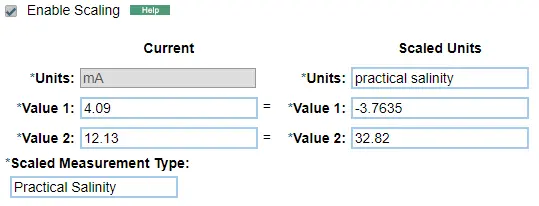
Image of the HOBOlink screen used to scale HOBO RX3000 sensor measurements.
For any questions or comments about this article or our products, please use the Contact Us button below.
Suggest an Article or Video Topic!
Recent Articles

How Glass pH Electrodes Work
In this video, learn about the electrochemistry that allows silver/silver chloride pH electrodes to measure the acidity of solutions. Modern electrode design is also reviewed to demonstrate what improvements have been made and what weaknesses are still present. Click...
STs Series Sensor Storage
STs Series sensors are constructed from high-quality, durable materials that can be stored for long periods of time. The only weak point is the electrode, which can be damaged or expire during storage in the wrong conditions. These conditions vary depending on the type of electrode, which is why we have different storage instructions for each sensor.
How a Glass pH Electrode Works
A comprehensive article covering how glass electrodes measure pH in a simple, understandable format. Specifically for silver/silver chloride electrodes.
