When to Calibrate and Replace an Electrode

Why is Calibration Required?
It is a simple question and a simple answer. Data is worthless if it is not correct, and calibration is required so we–the users–can verify that the electrode or sensor is giving us the correct data. It is one of the most important aspects of quality control and, in extreme cases, can cost tens of thousands of dollars and hours of time if even one electrode is off by 10%.
But you know all that. Why am I bothering to write this guide?
With the typical ego of a college graduate, I thought that the many laboratory classes taken to get a B.S. in Biology had thoroughly prepared me for the real world–or at least for basics like maintaining and calibrating an instrument. In general, I knew how to select and prepare buffers and perform a calibration, but there are many other factors not taught in school that affect the calibration process.
For example:
- What qualities of an electrode cause it to drift or become less accurate?
- How frequently is calibration required to maximize efficiency and accuracy?
- How is the health of an electrode determined quantitatively?
- When does an electrode actually require replacement to maximize value?
This guide goes over the specific qualities of pH, dissolved oxygen, ORP (redox), and conductivity electrodes that cause inaccuracies. It also covers questions 2-4 for any electrode.
Limiting Factors of Specific Electrodes
The reference solution is the limiting factor for most common types of electrodes. Rates of usage and contamination of the electrolyte depend entirely on how similar the chemical properties of the sample are to the reference solution. For example, an electrode in a low ionic solution will drift more rapidly compared to one in a high ionic solution because the reference electrolyte in most pH and ORP electrodes is 3.0M KCl–a high ionic solution–and the equilibrium force (and therefore dilution rate) is directly related to the difference between the reference and sample solutions.
Dissolved Oxygen Electrodes
Electrochemical dissolved oxygen electrodes are typically filled with a salt solution such as propionic acid. The electrodes typically have low diffusion rates so contamination is not a problem, but the salt solution does get used up eventually. Oxidation or reduction of the anode and cathode also become a problem over time.
Conductivity Electrodes
For contacting conductivity electrodes, such as the one in the pHionics STs Series Conductivity, the limiting factor is cleanliness of the electrode cells. Algae or dirt will build up and increase resistance between the cells, causing inaccuracies, especially for 2-cell electrodes (Learn about the different conductivity electrodes here!). pHionics conductivity electrodes are exceptionally durable so the build-up can be removed with soap and a soft brush or fine sandpaper without fear of damage.
When is calibration required?
Some common manufacturer statements are “Calibrate before each use.” or “Calibration schedule must be determined empirically.”
Very safe recommendations, but also very vague ones for industries where an electrode or sensor can be in use for days, weeks, or months at a time. Does “each use” imply each day in use, or perhaps each time the electrode is removed?
To remove the ambiguity, a system must be set up to quantitatively determine when calibration is required. There are two steps to this system:
- Perform consistent checks using a known calibration solution.
- To do this, dip the sensor in a known calibration solution for each parameter and verify that the output remains within acceptable range. Whenever the sensor is out of range then calibration should be done. These checks can be performed less frequently after the rate of drift is determined for the application.
- Consistently calculate the slope percent error and offset of the electrode during calibration to determine electrode health.
- This must be done with a two-point calibration and the exact steps are discussed later in the article.
“Consistent” is also vague, though, so let’s go through the factors affecting electrode drift and frequency of calibration.
Conditions Affecting Calibration Frequency
Likelihood of sensor contamination
- Sensors measuring liquids containing high levels of fats and oils will experience build-up and will require cleaning and recalibration.
Likelihood of sensor damage
- Sensors measuring liquids containing high levels of particulates may scrape the electrode and affect readings.
Sensor storage
- Storing a sensor in incorrect storage solution (such as low ionic solutions) may result in reduced electrode life and a greater rate of drift.
Accuracy requirement
- Some applications may require an accuracy within 0.5% which requires frequent calibration, while other applications only require an accuracy within 5%.
Determining a Calibration Schedule
For applications, such as laboratory measurements, where the sensor is only used periodically and is easily accessible, a calibration check (Step 1) once per day is recommended and should only require a few minutes at most.
For applications involving continuous monitoring, such as process control or wastewater treatment, it is best to perform a calibration check every 2-7 days (depending on how harsh the application is) when a sensor is first installed so that a baseline drift rate can be established. Once the sensor is nearing the extreme of acceptable error for an application, the sensor should be recalibrated and the time between first and second calibration recorded. This may be a week for some applications and a month for others. Knowing the time between calibration allows for a schedule to be created that ensures accuracy while also maximizing efficiency. Once a schedule is set up, calibration checks can be performed less frequently, averaging 0-3 times between full calibrations depending on accuracy requirements.
We recommend performing this process 3-5 times initially to get an average time between calibrations.
Click here for a full guide on creating a sensor maintenance schedule.
All electrochemical electrodes become less accurate over time, depending on how harsh the application is. With pHionics electrodes, typical life is between 6 months and 5 years with a 3-year average. This means that, starting a few months after the electrode enters service, the time that electrodes hold their calibration slowly decreases. We recommend that the time between full calibrations or checks is shortened periodically as electrode health declines. The following sections go over how electrode health is calculated.
Calculating Electrode Health
Two-Point Calibration
Measuring sensors are always based on assumptions. No matter how much we calibrate, there will always be some difference from the theoretical values because real-life factors influence the readings. We can get close though, and the best way to do so is by measuring points at either side of the expected sample range followed by interpolation of the information using theoretical equations.
It would be great if only one buffer solution, such as a pH 7.0 buffer, could be brought to the site to test calibration, but a single point calibration only guarantees that the sensor will accurately read at that point, meaning that even if the sensor reads 7.0 pH perfectly, it may have significant drift for every other pH measurement. Multiple calibration points should be used for pH measurements, but calibration for ORP, dissolved oxygen, and conductivity generally only require one point except when calculating slope and offset. This may change depending on the accuracy requirements of each application.
While it would be most accurate to take calibration points at intervals across the entire range being measured, two-point calibration is generally used because it can provide high accuracy without the time commitment and resources of using 5-10 known calibration solutions. We always recommend setting one calibration point above the expected measuring range and one below as interpolation is more accurate than extrapolation.

Figure 1: Theoretical vs Actual pH Slope and Offset. This graph may have different axes than typical sensor calibration graphs seen before because pHionics sensors have transmitters included in the body, translating the output from millivolts to 4-20mA. The combination of sensor and transmitter in one body improves noise reduction to increase accuracy.
Calculating Slope and Offset
Once the two readings of known measurements have been recorded then you can calculate slope percent error and offset. The offset will tell you how far away the actual slope is from the theoretical slope and help determine when the electrode requires replacement. If the electrode has been properly calibrated and cleaned based on our guidelines (Click here for pHionics STs Series Device Manual) and the slope percent error is still outside of the accepted range of ±15%, then the electrode should be replaced. In general, the greater the offset, the less time the electrode will remain calibrated.
If a replacement electrode is not within the allowable budget or not available at the time, a calibrated sensor outside of the accepted offset can still be used but will require more frequent maintenance as the drift rate will be higher.
Clarification: The slope percent error indicates the health of the electrode and not the accuracy. Having a slope percent error of 10% does not mean that the pH readings obtained from the sensor are off by 10%.
The equations for calculating slope, theoretical slope, percent error, and offset have been included below along with an example calculation.
Actual Slope Equation

Theoretical Slope Equation
For readings that are converted to a common analog output such as 4-20mA or 0-5V, simply divide the output range by the total parameter range (e.g. 0-14pH) to obtain the theoretical slope for the given sensor.

Percent Error Equation
The percent error is determined by dividing the difference between theoretical and actual value by theoretical value, then multiplying by 100 to obtain the percentage.
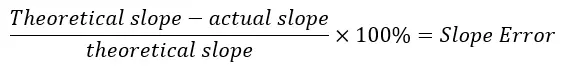
Offset
We also want to see how far off one point is from the theoretical ideal value. Typically the midpoint output of the sensor range (12.00 mA output for pHionics instruments) is used and the acceptable offset for pHionics instruments is ±0.60 mA.
Example
pH calibration is done with three known buffer solutions at 4, 7, and 10 pH. As the expected sample range is between 5-6 pH, we would calibrate the instruments using the pH 7 solutions first, followed by pH 4. All pHionics devices use a 4-20 mA analog output to communicate with dataloggers and controllers so the outputs we receive are 12.09 mA in pH 7 solution and 8.53 mA in pH 4 solution. We then divide the difference between the readings over the difference between the pH to obtain the slope of the line. Following that, we compare how close the actual slope (1.187 mA per pH) is to the theoretical slope (1.14 mA per pH) and calculate the percent error. The offset is calculated based on the difference between actual and theoretical mA output at 7 pH.

The acceptable range for slope error is ±15% and acceptable offset is ±0.60 mA so the electrode is ready for sample measurement.
Changing a Calibration Schedule Based on Calculated Offset
Take, for example, a sensor involved in wastewater treatment that is shown to drift out of acceptable range once every four weeks. The plant operator performs a calibration check once a week (3 total between calibrations) and notices that the sensor seems to be nearing the limits of accuracy after the check during the third week. The plant operator cleans and calibrates the sensor ahead of schedule and notes the change.
As the change could be due to the electrode stability declining or changes in the solution being measured for that period, the operator does not initially change the time between full calibrations. Instead, more checks are done during the next period, and the operator finds the sensor nearing acceptable accuracy limits early again. At this point, the operator cleans and calibrates the sensor with a two-point calibration and notices that the slope percent error has changed from -4.1% to -6.3%, indicating reduced electrode health. They move all future calibrations up one week.
The following month they see electrode health decrease again and extrapolate when the electrode will become unusable, then place an order for a new electrode.
Other Factors Affecting Accuracy
Calibrating a sensor properly does not, unfortunately, guarantee accuracy. Outside factors such as background noise from electromagnetic interference or ground loops are common and not easily fixed, resulting in wasted time and money. pHionics exists to remove those outside problems and simplify accurate water quality measurement with numerous features built into every product. If you are in the market for pH, ORP (redox), dissolved oxygen, or conductivity sensors and transmitters, the pHionics STs Series™ is here to provide you with a high-quality, long-lasting solution.
Conclusion
Hopefully, this guide proves helpful by providing quantitative methods for calibration and electrode replacement scheduling. As always, pHionics is here to give you resources and products that save you time and money. For any questions or comments, please contact us by clicking the Contact Us button below.
